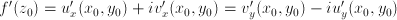Ecuaciones de Cauchy-Riemann
Mira otros diccionarios:
Ecuaciones de Cauchy-Riemann — Saltar a navegación, búsqueda Las ecuaciones de Cauchy Riemann son dos ecuaciones diferenciales parciales que son básicas en el análisis de funciones complejas de variable compleja, debido a que su verificación constituye una condición necesaria… … Wikipedia Español
Teorema de Cauchy — Numerosos teoremas deben su nombre a Augustin Louis Cauchy: El teorema integral de Cauchy en análisis complejo, generalizado al teorema de Cauchy Goursat. Véase también la fórmula integral de Cauchy. El teorema del valor medio de Cauchy en… … Wikipedia Español
Bernhard Riemann — Para otros usos de este término, véase Riemann (desambiguación). Bernhard Riemann Bernhard Riemann, 1863 Nacimiento … Wikipedia Español
Historia de las ecuaciones diferenciales — Una ecuación es una igualdad condicional que se cumple sólo para las soluciones de la misma. Así, en una ecuación algebraica como x – 2 = 0, la igualdad sólo se cumple para x = 2. En forma similar, una ecuación diferencial, constituida por… … Wikipedia Español
Logaritmo complejo — Una única rama del logaritmo complejo. El tono del color se utiliza para mostrar el argumento (ángulo de coordenadas polares) del logaritmo complejo. La intensidad del color se utiliza para mostrar el módulo del logaritmo complejo. La página con… … Wikipedia Español
Función holomorfa — Las funciones holomorfas son el principal objeto de estudio del análisis complejo; son funciones que se definen sobre un subconjunto abierto del plano complejo C y con valores en C, que además son complejo diferenciables en cada punto. Esta… … Wikipedia Español
Variedad compleja — En geometría diferencial, una variedad compleja M es una variedad topológica que tiene la estructura que nos permite definir la noción de función holomorfa .[1] Ello se podrá conseguir por dos caminos: Exigiendo que exista un atlas (o conjunto de … Wikipedia Español
Teorema de los residuos — El Teorema de los residuos es consecuencia directa del Teorema integral de Cauchy y forma parte fundamental de la teoría matemática de Análisis Complejo. Contenido 1 Enunciado 2 Demostración 3 Véase también … Wikipedia Español
Función armónica — En matemáticas, sea f : D → R (donde D es un subconjunto abierto de Rn) una función real de n variables, se la llama armónica en D si sobre D tiene derivadas parciales continuas de primer y segundo orden y satisfacen la ecuación de Laplace… … Wikipedia Español
Anexo:Matemáticos importantes — En esta lista de matemáticos importantes se presenta una selección de matemáticos desde la antigüedad hasta el presente. La selección se orienta por los aportes científicos, utilizando como criterio para definir el grado de notoriedad la atención … Wikipedia Español
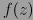 , con
, con 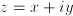 y
y 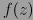 se puede descomponer en suma de dos funciones reales de dos variables u y v, de manera que
se puede descomponer en suma de dos funciones reales de dos variables u y v, de manera que 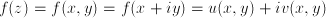 . Si la función
. Si la función 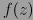 sea derivable en un punto
sea derivable en un punto 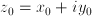 entonces deben verificarse las condiciones de Cauchy-Riemann:
entonces deben verificarse las condiciones de Cauchy-Riemann:
 Además se cumple que el valor de la derivada en el punto, de existir, debe ser:
Además se cumple que el valor de la derivada en el punto, de existir, debe ser: